Shortcut on the Way to Freeform Optics
Published in: Kunststoffe International 12/2013, page 58-61
Authors: Lars Dick (Jenoptik Polymer Systems GmbH) und Laura Florez
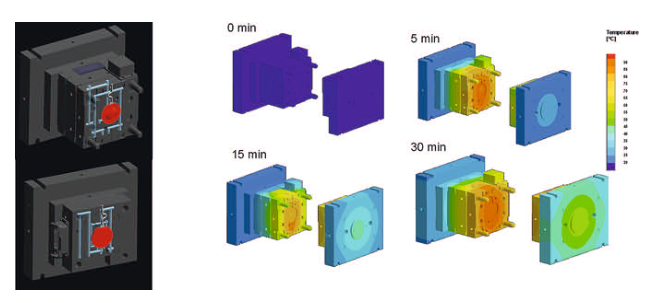
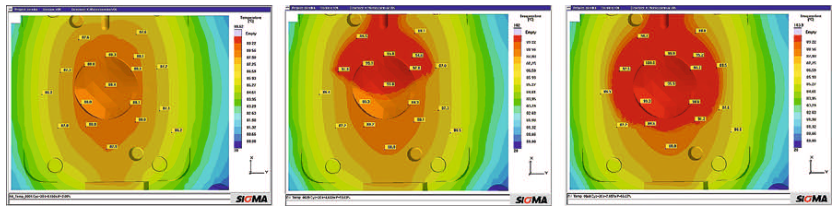
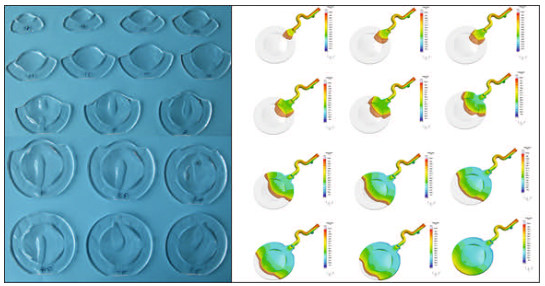
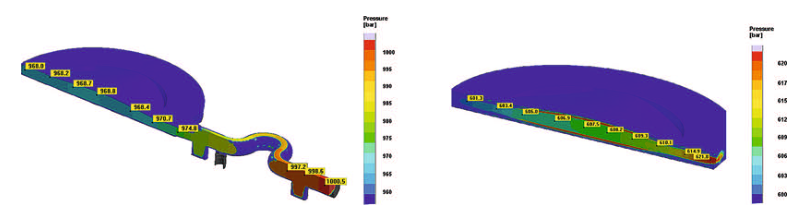
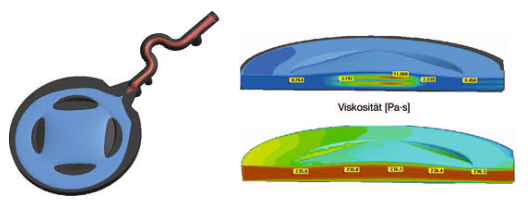
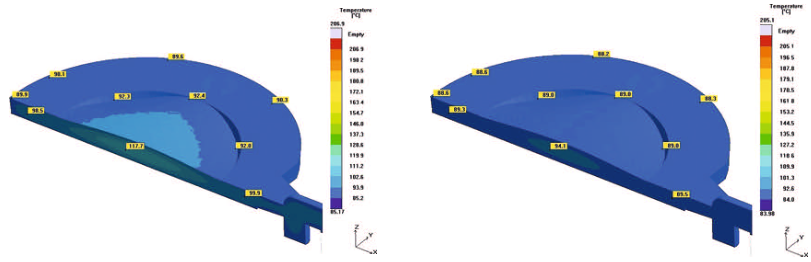
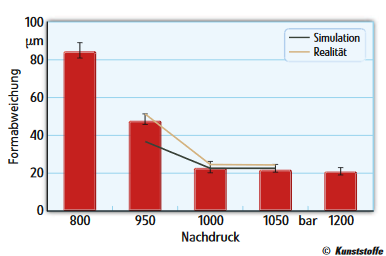
Virtual Mold Trials. The manufacture of plastic optical components usually involves a highly iterative process during development of the molded part and mold construction. Reason for this is the uncertainty associated with the injection molding behavior. The case example from a research project demonstrates how a virtual mold trial can replace this stepwise approach, which also results in considerable cost reductions.
Optical components manufacturing is one of the most demanding tasks for injection molding. Precise dimensions, tight tolerances, and the persistent demand for faultless and reproducible parts represent the operational framework in this industry. Driven by increasing miniaturization and more functionality in new device generations in the past years, the industry has shown a strongly increasing demand for high-precision injection molded optical components. Analogous to the innovative impulses for new, more compact equipment system triggered in recent years through the functional options of aspheres, new perspectives for future system innovations are presently emerging through the use of application-specific freeform optics. This nomenclature summarizes refracting and reflecting surfaces that clearly differ from symmetric and aspheric geometries.
However, due to inadequate availability of technical basics, today's demand for plastic types for freeform optics can only be met at uneconomic expense. Within the scope of the FREE project – the acronym stands for “precision freeform optics” – Jenoptik Polymer Systems GmbH in Triptis, Germany, was faced with the challenge of producing symmetric, non-rotation freeform optics from high-performance plastic materials. Hereby, the aim was to achieve a precision of 0.5 µm. In order to penetrate this lucrative business, in which polymerbased precision optics with symmetric, non-rotation freeform profiles play a key role, this project was to create the required basic competences.